This was a post from my old blog. Some links/formatting/images may be out of date.
I can't release the original source used for this (which was written in C++), but I have a very similar implementation in C# from a different project that I've posted in full here: https://gist.github.com/redxdev/0ce846f5c7e1edc36e7c5148109d53af
The links in this post have been updated to point to the new C# implementation.
Note that each image in this post is from a separate run of the generator.
This is going to be a quick article about procedural dungeon generation in unreal engine. I recently came across this article on Gamasutra, which describes a really cool dungeon generation algorithm used by TinyKeep. I decided I wanted to try implementing it in Unreal Engine 4, so here are some notes on my attempt.
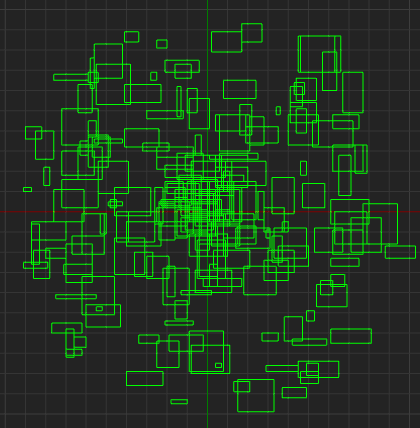
This is the first step of the generation process: Create a large number of randomly sized regions within a circle. Note that they are green in this image as green represents "default" regions, which don't yet have a purpose.

Next comes separation. I don't want any of the regions overlapping, so I used a simple separation steering behavior. The Gamasutra article uses a physics engine to do this part, but I see that as unnecessary and over the top for what could be a very simple algorithm. Using a physics engine also means you don't get nearly as much control over the results, so I went with the original way TinyKeep used.
Here are the basics of the separation algorithm I used. The main thing to note is that I only apply separation to a region based on what other regions are overlapping. In my actual code, there's also a bit that keeps track of how many "ticks" separation has occurred for (how many times it has gone through the while loop), and if that number gets too large then it breaks out of the loop so that we don't end up with an endless loop situation. There's some inefficiency in the code as the number of checks for separation grows exponentially with the number of regions, and it could easily benefit from some sort of spatial partitioning, but it still runs fairly fast and doesn't need to be too efficient since this is meant to run during a loading screen as opposed to while the game is being played.

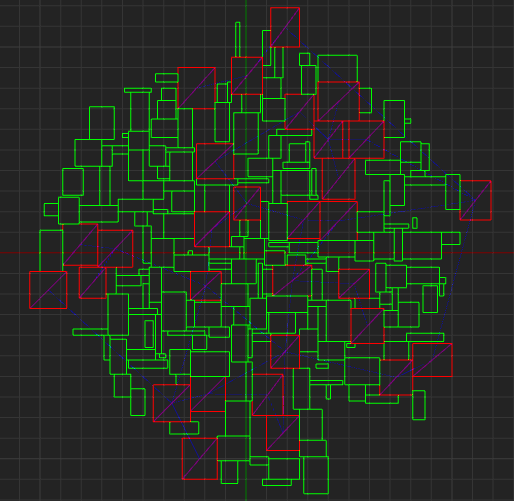
Here's where I start assigning purposes to different regions. I find the average size of the regions, then find the set of all regions above that size * a multiplier. I mark all regions in that set as "main" regions, which are highlighted in red. These will be used to figure out how the hallways of the dungeon should be generated.

It may be a bit hard to see in the above image, but there are blue lines creating a graph of all main regions. This graph is the Delaunay triangulation of the centers of each main region. This will be used in the next few steps to create hallways. To actually generate the Delaunay triangulation, I used this code, modified to use Unreal Engine's constructs (such as FVector2D) (Update: The code in this post is in C# and not meant to work with Unreal anymore).

Now it is really hard to see, but the blue lines are still there. There are quite a few less of them, and that is because this is a minimum spanning tree of the previous graph. This guarantees that all main rooms are reachable in the graph, while also not duplicating any paths. I used Prim's algorithm since it was simple to implement. Here is my implementation, and again it would probably benefit from some better data structures but it is fast enough for my purposes.
The problem with the MST is that it makes a fairly boring dungeon where every path leads to a dead end. It works as a starting point, but there should be some cycles in the main region graph. As such, I randomly choose some edges from the original triangulation graph that aren't a part of the MST and add them to the final graph.

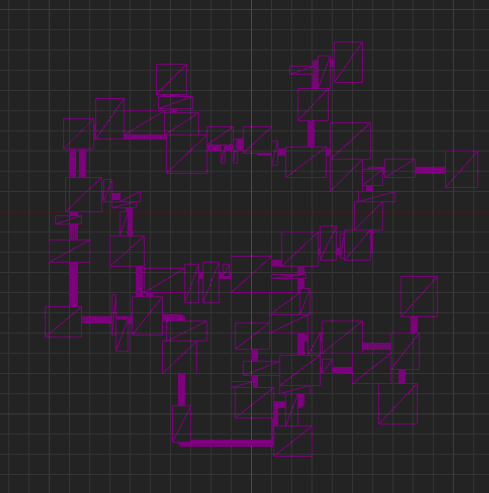
Here you will notice that all of the green regions are now black. This is because I've set their type to "none". Regions of type "none" will be deleted completely from the dungeon when the algorithm completes, so I set everything that isn't a main region to "none". You'll also notice that the blue lines now create corners and always follow the X or Y axis. This is because they will be used to create the final hallways that connect the main rooms. The algorithm to figure out how to lay out the lines for hallways is pretty simply and explained in the Gamasutra article, but here's my implementation.

Now I find the intersection between each of the blue lines and the unused regions, then add them back in to the dungeon. They are highlighted in pink here because they are marked as hallways. You will notice that doing this still doesn't connect all regions together, which is why the next step happens...

Look at all those tiny pink squares! I do a check around each line to find any space that isn't taken up by any region, then fill that in with a small hallway region. Ideally this would have another step which optimized regions of the same type that are adjacent into a single region, but that's a topic for another day.

The final two steps are show here: The first is to remove any unused regions, and the second is to "tag" regions as needed. Regions can have tags which is used to define what a region is used for. Right now, there are only three tags defined: None, Start, and Exit. None is applied to everything by default, while Start and Exit are applied to main regions. Right now the generator chooses a random main region for the Start tag, and then finds the furthest main region from that one and uses it as the Exit tag.
That's it for the dungeon generation algorithm. All that is left is to actually spawn geometry, which is something I am still working on.
Here's a link to the C# implementation once again, it should be fairly easy to port to most engines/languages/etc: https://gist.github.com/redxdev/0ce846f5c7e1edc36e7c5148109d53af